
Models, Metaphors, Examples and Instruction
Many people have asked me over the years why I so often use the phrase ‘models, metaphors, examples and instruction’ when talking about mastery approaches to teaching. This short blog is a high-level response to that question.
Within every mathematical idea, problem or situation lies technical detail. This technical detail is key to allowing anyone learning mathematics to be able to take part in The Great Conversation of mathematics, such that they are not simply a passive recipient of the subject, but rather are in a position to contribute meaningfully and identify subterfuge. Study of this technical detail is akin to the study of grammar of the English language.
"Grammar is important because it is the language that makes it possible for us to talk about language. Grammar names the types of words and word groups that make up sentences not only in English but in any language. As human beings, we can put sentences together even as children—we can all do grammar. But to be able to talk about how sentences are built, about the types of words and word groups that make up sentences—that is knowing about grammar. And knowing about grammar offers a window into the human mind and into our amazingly complex mental capacity."
"People associate grammar with errors and correctness. But knowing about grammar also helps us understand what makes sentences and paragraphs clear and interesting and precise. Grammar can be part of literature discussions when we and our students closely read the sentences in poetry and stories. And knowing about grammar means finding out that all languages and all dialects follow grammatical patterns."
Haussamen, Brock, et al. "Some Questions and Answers About Grammar," 2002
Technical detail in mathematics makes it possible for us to talk about mathematics.
Here is a mathematical problem:
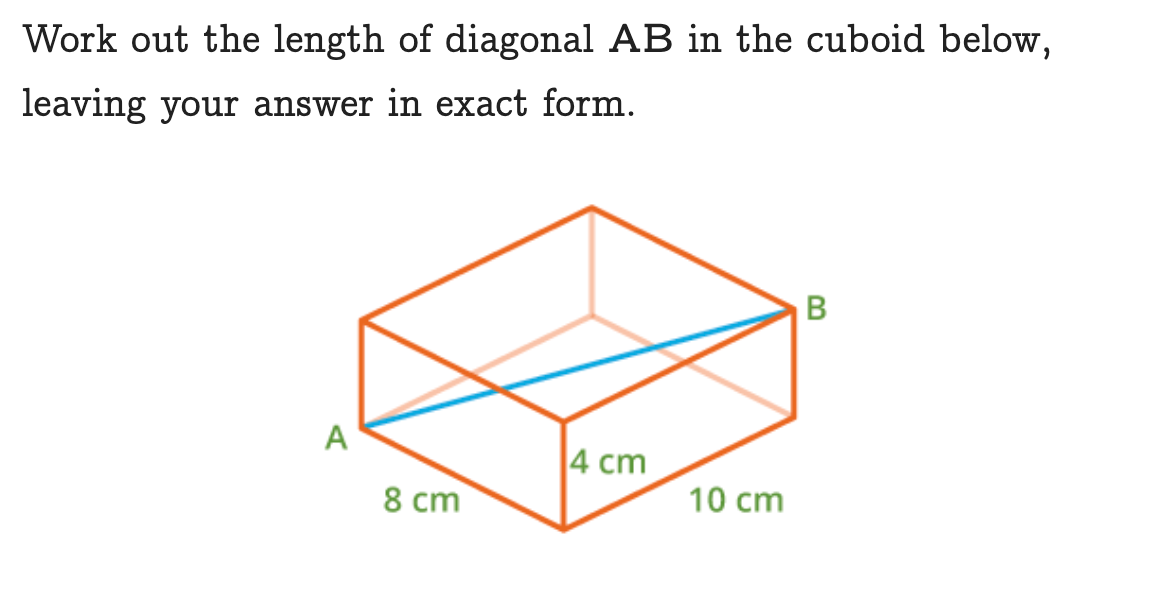
It is not enough for the teacher of mathematics to consider this problem to be self-contained within a single lesson titled ‘Pythagoras’ Theorem’. The teacher is able to consider the problem from this perspective because they have an often-unconscious appreciation of the technical detail that lies beneath, which enables them to talk about this problem as though there is only one technique at play. Yet there are many. Here is some of the technical detail that makes up this seemingly routine Pythagoras question (this is not intended as an exhaustive list, but hopefully conveys the point):
Equals
The equals symbol, ‘=’, denotes that, for any two given expressions, applying an isomorphic function to each will maintain equality. Teachers should continually reinforce in pupils’ minds that the equals symbol gives them permission to ‘break and fix’ equality in any way they choose. Fixing merely requires applying the same function that has been applied to one expression to the other.
Equality
Two expressions have equality if they have the same value or represent the same mathematical object.
Equivalence (relation)
A binary relation that is reflexive, symmetric and transitive. These three conditions must be met:
-
- a = a (reflexive property),
- if a = b then b = a (symmetric property)
- if a = b and b = c then a = c (transitive property)
Equation
An equation is a mathematical statement asserting that two expressions have equality.
Area
The area is the extent of a 2D shape on a plane. This can be given a numerical quantity to communicate its extent in relation to standard extents. At school level mathematics, the archetypal area unit is a square. All areas can be defined in relation to the archetypal area unit. This archetypal unit can be chosen to best fit the scenario (for example, a square of 1mm by 1mm, a square of 1cm by 1cm, a square of 1m by 1m, and so on to fit the circumstance)
Addition
Addition is of the two key operators required to create a mathematical field. Addition has key properties as expressed in the Field Axioms.
Multiplication
Multiplication is of the two key operators required to create a mathematical field. Multiplication has key properties as expressed in the Field Axioms.
Commutativity
The characteristic of equality being maintained when the order of an operand is changed. Addition and multiplication are commutative. For example, 2+5 and 5+2 have the same value, 5x6 and 6x5 have the same value. When teaching both addition and multiplication, teachers should continually stress that the operations are commutative and use varied examples to expose the commutativity of these operators repeatedly.
Inverse function (anti-function)
An inverse functions returns the output of a function to its original form. When teaching, teachers can use the analogy with pupils that an inverse function ‘reverses’ or ‘undoes’ a function. Teachers should use varied example, on many occasions throughout the curriculum, to demonstrate the impact of an inverse function. For example:
-
- adding 5 can be undone by subtracting 5
- multiplying by 8 can be reversed by dividing by 8
Formally:
If the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, and vice versa, i.e., f(x) = y if and only if g(y) = x
Exponentiation
A mathematical operation with a power, n, acting on a base, b. This can be written as bn. In the case where n is a positive integer, the action corresponds to repeated multiplication. For example, bn = b x b x b… x b, where the multiplication has been performed n times. For example, 45 = 4 x 4 x 4 x 4 x 4 = 1024.
nth root
In the equation, rn = x, the nth root of x, n, has the value r. When teaching nth root, teachers should first ensure pupils fully understand exponentiation. The nth root can then be discussed in terms of familiar exponent scenarios. For example, given that pupils are comfortable with the fact that 23 = 8, teachers can then discuss finding the number which gives 8 when raised to the power 3.
Plane angle
The figure formed at the common point shared by two rays.
Turn
Turn is the archetypal unit of plane angle. At school level mathematics, the most common values used to represent this unit are 360 degrees or 2 radians. Teachers should continually reinforce that one full cycle is a unit of turn.
Comparison
Expressions can be stated to be equal when they have the same value or represent the same mathematical object. When expressions are not equal, their relative values can be compared by stating whether the value of one expression is greater than or less then the value of another expression. This gives a range of comparisons which can be made
-
- Equal to
- Greater than
- Less then
- Greater than or equal to
- Less than or equal to
Isolate
To manipulate an equation such that one expression is a single variable. This is sometimes referred to as ‘transposition’ or ‘making x the subject of the formula’, where ‘x’ is the variable to be isolated. The ability to isolate is key to being able to solve equation problems or evaluate formulae. Teachers should rehearse this skill regularly with pupils. Often, a pupil who appears unable to work with equations or formulae, is actually struggling to isolate.
Plane
A two-dimensional surface extending to infinity.
Operation
A calculation from zero or more input values to an output value. At school level mathematics, pupils work with unary and binary operations. Unary operations, such as trigonometric functions, involve only one value. Binary operations, such as addition, multiplication and exponentiation, involve two values.
Function
A process for relating every possible value in a set to exactly one value in another set.
Set
A defined collection of objects.
Field Axioms
Just nine properties provide the basis for all of arithmetic and algebra. The axioms of a field – or, as often stated, the field axioms – give the mathematician a rules-based approach to working with number and variables. Knowing and being able to work with the field axioms means that a pupil can attack any arithmetical or algebraic problem they might face in school-level mathematics. These properties always hold true; they are the same properties at the beginning of primary mathematics as they are at the beginning of calculus. They hold for whole numbers, fractions, negative numbers, rational numbers, letters and expressions.
Establishing their truth and utility is therefore the key aim of the teacher of early-stage mathematics.
The nine field axioms are split into properties for addition, properties for multiplication and a property connecting addition and multiplication. It is important to note that none are presented as subtraction or division.
The properties of addition:
|
Axiom |
Description |
Symbolically |
|
1 |
Associative property of addition |
(a + b) + c = a + (b + c)
Example: (2 + 3) + 4 = 2 + (3 + 4) |
|
2 |
Commutative property of addition |
a + b = b + a
Example: 2 + 3 = 3 + 2 |
|
3 |
Additive identity property of 0 |
a + 0 = 0 + a = a
Example: 3 + 0 = 0 + 3 = 3 |
|
4 |
Existence of additive inverses |
For every a there exists –a so that
Example: 2 +(–2) = (–2) + 2 = 0 |
The properties of multiplication:
|
Axiom |
Description |
Symbolically |
|
5 |
Associative property of multiplication |
(a × b) × c = a × (b × c)
Example: (2 × 3) × 4 = 2 × (3 × 4) |
|
6 |
Commutative property of multiplication |
a × b = b × a
Example: 2 × 3 = 3 × 2 |
|
7 |
Multiplicative identity property of 1 |
a × 1 = 1 × a = a
Example: 3 × 1 = 1 × 3 = 3 |
|
8 |
Existence of multiplicative inverses |
For every a ≠ 0 there exists 1/a so that a × 1/a = 1/a × a = 1
Example: 2 × 1/2 = 1/2 x 2 = 1 |
Connecting addition and multiplication:
|
Axiom |
Description |
Symbolically |
|
9 |
Distributive property of multiplication over addition |
a × (b + c) = (a × b) + (a × c)
a(b + c) = ab + ac |
Dimension
The minimum number of coordinates required to specify a point in a mathematical space. Pupils’ early encounters with dimension include specifying a point on the number line, which requires only one coordinate and so is said to be one dimensional.
Coordinate system
A system for uniquely identifying the location of a point or points. Pupils’ early encounters with coordinate systems include specifying a point on the number line. Teachers should build on pupils’ familiarity with and understanding of the number line when introducing Cartesian coordinate systems.
Value
Any definite mathematical object. At school level mathematics, pupils most common encounter with mathematical objects will be as numbers. Numbers are values.
Magnitude
The relative size of a mathematical object. Magnitude can be described using comparison.
Ratio
For any two given entities with numberness, ratio is a relationship stated numerically of how many multiples of the first entity compare to the stated multiples of the second entity in a given context. For example, a class containing 13 girls and 8 boys could be described as the relationship of girls to boys as 13:8.
Numberness (numerosity)
A set of physical objects is said to have numberness if the objects can be counted.
Number
A mathematical object used to count, label, measure, compare, order or discuss items that have numberness.
Numeral
A symbolic representation of numberness.
Digit
Individual symbols in a given base system used to create numerals.
Radix (base)
The number of unique digits used to represent numbers. At school level mathematics, pupils work mainly Decimal (a system with radix of ten), using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to create numerals. The teaching of multi-base arithmetic is critical is pupils are to true grasp the meaning of place value and, therefore, how algebra is used to communicate working in an unknown base. When pupils are secure in working across different radix systems, they are able to make strong connections across arithmetic and algebra, giving them the power to work in the generalised form with meaning.
Place Value
The relationship, in a given radix (base) system, between numbers, numerals, digits and numberness.
Fractionness
The existence of equal parts
Simple fraction (common fraction or vulgar fraction)
A rational number, expressed as a/b, where a and b are integers and b is not equal to zero.
Quantity
A magnitude or multitude. Quantities can be mathematical objects or physical objects.
This technical detail matters enormously, not just when attacking the problem personally, but fundamentally when teaching pupils about these types of problems. It is not enough for the teacher to have expert mathematical knowledge, rather the teacher needs to have expert knowledge in how to enable a pupil to gain meaning and understanding of the novel idea, which means the teacher must be alert to all of the technical detail involved in any given problem or topic.
James Fey considered this preparing of technically detailed and true mathematics for the teaching process as one of ‘elementarization’. As Fey puts it, “the translation of mathematical concepts, principles, techniques, and reasoning methods from the forms in which they are discovered and then verified by formal reasoning to forms that can be learned readily by a broad audience of students.”
This is a fact that is too often absent from mathematics teacher training and professional development; there needs to be some ‘translation’, some process, some experience that enables a novice to grip an idea and that this ‘translation’ necessarily requires considering the mathematics in a different way to its technical truth. We require a medium in order to communicate the mathematics.
I think of this as didactics of the mathematics. The range of actions teachers take in order to transfer an idea known to them into an idea known to the pupil with technical accuracy.
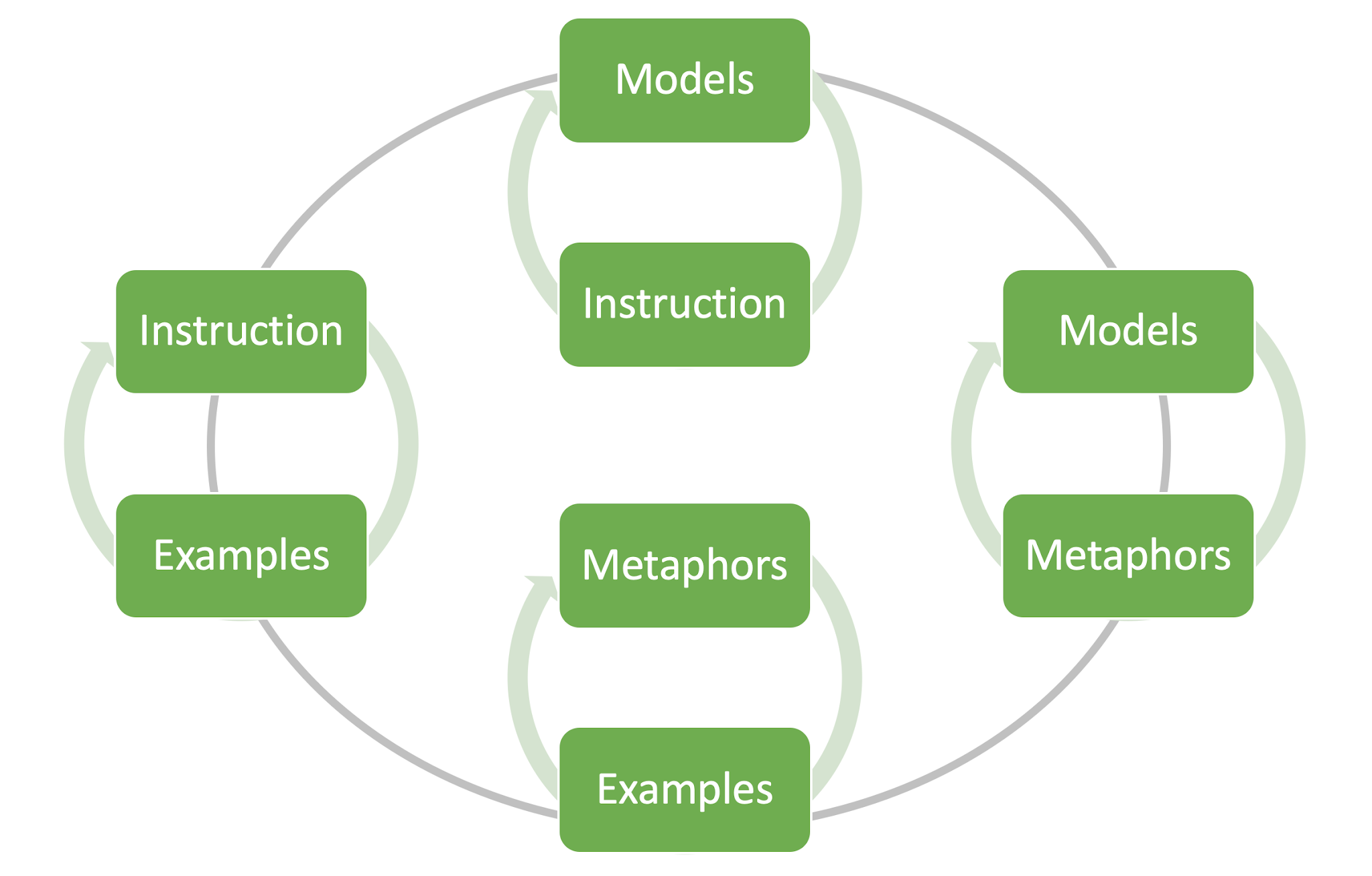
I suggest an element of this didactics of the mathematics as the hierarchy
Models
Metaphors
Examples
Instruction
I choose these words to label some phases of action. They could easily be different words, but I have mulled it over for years and think these words work well.
I introduced this idea above as a hierarchy, but actually, I don’t even believe this myself! This is much more like Hemel Hempsted’s Magic Roundabout, with mini-cycles inside a cycle.
Beginning at the base layer. Instruction is the way in which the teacher communicates an idea in front of a class or pupil. It is the words they use, the hand gestures, the sentences, the body language. It is the images they draw and where they point when talking about them, it is the time they take and the pauses they throw in. Instruction is one key element of a teacher’s pedagogy. But pedagogy without didactics is mere performance. Instruction is how teachers introduce and speak about the examples they will use.
Examples are the questions teachers pose and the batting to-and-fro with pupils as they undertake their own attempts on examples and articulate to the teacher their thought processes. They are the in-the-moment tweaks and changes that teachers make in response to these articulations and they are the pathway to automaticity and fluency. Examples are the way in which teachers convey the metaphor they are hanging the new meaning around.
Metaphors are the connective stories that teachers use to convey novel information from a viewpoint of a pupil’s familiarity. They are the everyday, they are the common sense, they are the narrative. Metaphors make it possible for the novice to comprehend surprising, disruptive and difficult new knowledge. Metaphors are communicated through models.
Models are the words, images, apparatus, tools and dynamic representations of mathematical ideas that enable teachers to discuss the chosen metaphor. They are the ways in which pupils manipulate, rearrange and converge towards new insight.
We choose an appropriate model for the metaphor that we have chosen. We choose our metaphors because we know our pupils. The choice of models and metaphors determine the choice of examples that we will use with our pupils. And the choice of model, metaphor and example at any given moment informs our approach to instruction.
So perhaps the ‘hierarchy’ looks something like this:
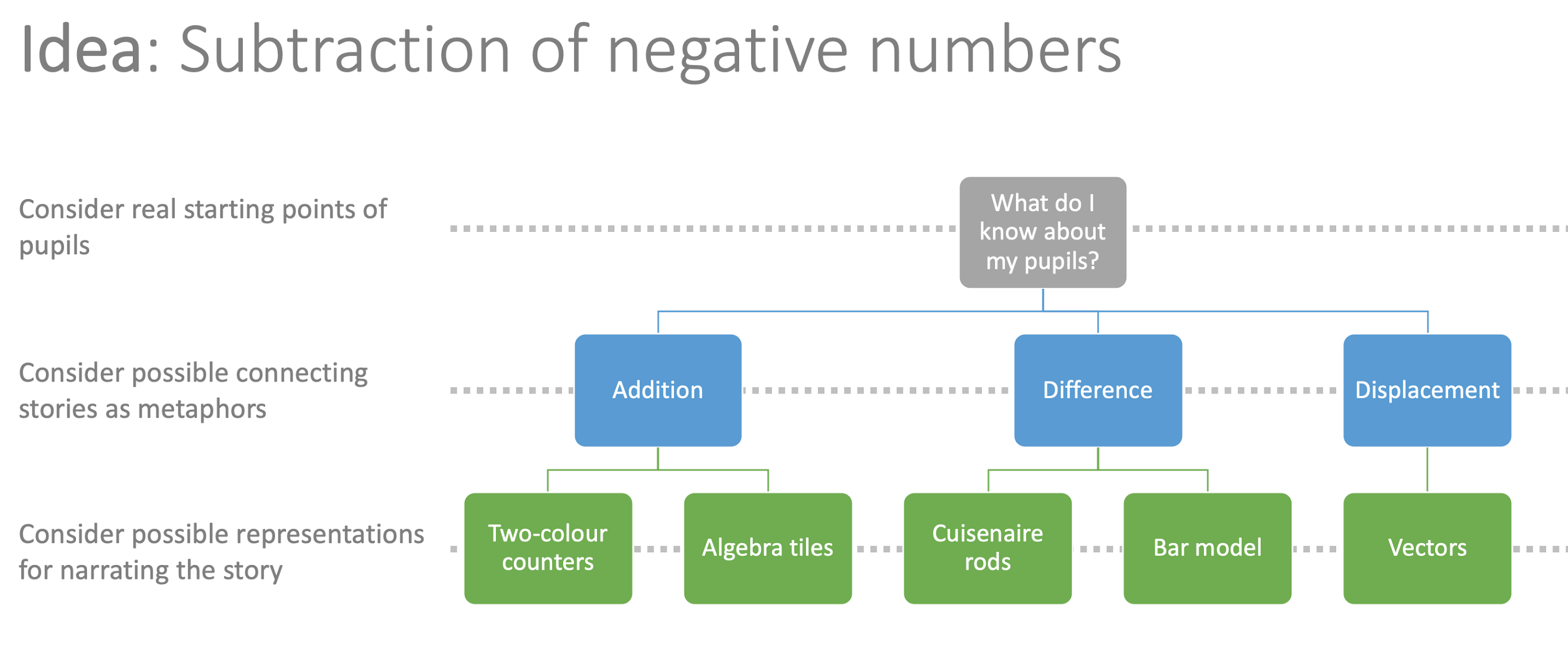
Let’s consider an example. Suppose, for instance, the prima facie idea at hand is ‘subtraction of negative numbers’. Just like with the problem above, which appeared on the face of it to be about Pythagoras’ Theorem, any problem in the idea ‘subtraction of negative numbers’ will also have technical detail at its heart. Here, though, I want to look at an example of the ‘hierarchy’.
How do I start the thinking process? How do I get to a point where I can perform an impactful translation from what I already know to be technically true, through a medium, to convince a pupil of what is technically true?
To begin with, I think about my pupils and what I know them to be already familiar with. This gives me the beginnings of my story telling. The beginnings of choosing my metaphor.
For this particular idea, there are three metaphors that I think will work with my pupils:
- Addition
- Difference
- Displacement
I choose these because I know that my pupils are familiar with all three, which means I can bridge from the familiar to the unknown by telling a connected story, in a logical and precise way, through the use of models, examples and instruction.
Suppose I choose addition as my metaphor. This requires the introduction of the idea of additive inverse. I know I am able to do this, because I know my pupils have been mathematically conditioned to be comfortable with the idea of doing and undoing. I can now choose a model to convey this metaphor. If dealing simply with numbers, I will choose to use two-colour counters, if dealing with the general case, I will choose to use algebra tiles. This model is chosen carefully to enable the pupil to see the logic in the technical detail of additive inverse – they can see and appreciate the existence of zero pairs.
Suppose I choose difference as my metaphor. I know I am able to do this, because I know my pupils have been mathematically conditioned to be comfortable with comparing. There are several models I could choose, but my go-to choice would be either Cuisenaire rods or a simple pictorial bar model.
Suppose I choose displacement as my metaphor. I know I am able to do this, because I know that my pupils have been mathematically conditioned to be comfortable with the ideas of movement, comparing and doing and undoing. The model I would choose here would be that of vectors.
So, by knowing my pupils, I can make choices about metaphors, which in turn determines the models I have available to me, which in turn authors my examples and determines the words, gestures, pauses and detail of my instruction.
The hierarchy also serves us well when we wish to engage with ‘corrective’ teaching. That is to say, when a pupil has not yet gripped an idea and we undertake some new actions to remedy this. I do not for one minute buy the common protest, “oh that kid doesn’t get it” or “this pupil isn’t very good a mathematics.” Either we believe that teaching can have a profound impact or we do not. I, for one, am firmly in the former camp. All pupils can learn well given the right conditions and their sincere effort.
Suppose we are in the game of tennis that is batting questions back and forth with a class as examples and problems. And we are listening to them articulate their thinking when we spot a moment of confusion or error.
The hierarchy acts as a check list for action taking. Rather than the typical practice that is often seen in mathematics classrooms, where a teacher reacts to a pupil ‘not being able to understand’ algebra tiles, say, by immediately changing the model, we can use the hierarchy to more carefully consider corrective teaching.
So, if a pupil has not gripped an idea, let’s start at the base layer. Was there some aspect of my instruction that was unclear or muddled? Did I demonstrate the use of the model accurately and avoid misconception? Was my emphasis appropriately timed to draw pupils’ attention to the most important aspects?
We can then choose to change our instruction.
If confident that the instruction is not the issue, the next layer can then be considered. Have the examples and problems been chosen well? Do they reveal underlying relationships? Do they rely on knowledge the pupils have in order to complete calculation? Are the variables suitably selected? And so on.
We can then choose to change our examples.
If confident that the instruction was clear and accurate and that the examples are known to be effective, then to the next layer…
Did I choose a suitable metaphor? Did I really take into account my pupils’ true starting points and foundational knowledge? Is the metaphor known to be impactful for communicating the mathematical idea at hand?
I can then choose to change the metaphor, which, of course, necessitates the changing of the model.
In sum, I so often use the phrase ‘models, metaphors, examples and instruction’ because I think it acts as a helpful framework in creating the actions and the medium through which teachers can create pedagogy with didactics classrooms rather than classrooms that focus purely on pedagogy with no regard to technical detail and the need to translate one’s own mathematical knowledge into a form that can be received by pupils. Pedagogy without didactics is mere performance, pedagogy with didactics ensures all pupils can learn well by building accurate, technical detail.
It is not enough to merely expose pupils to what Matthew Arnold famously referred to as ‘the best that has been thought or said’. That is no education. What I want for pupils is for them too to have the mechanisms and technical knowledge that make them able to be the adults who think and say the best. This means they must study the grammar of mathematics – its technical detail – so that they, themselves, can speak about the mathematics.